Contoh Soal PM UTBK 2023 dan Pembahasannya – idschool.net

PM adalah sebutan untuk Penalaran Matematika. Merupakan salah satu subtes UTBK pada SNBT 2023. Ada 10 contoh soal PM UTBK 2023 dari halaman simulasi-tes.bppp.kemdikbud.go.id pada waktu. Salinan kesepuluh contoh soal UTBK 2023 dan pembahasannya ada di bawah.

Daftar isi:

Baca Juga: Rekomendasi buku UTBK 2025 Terbaik untuk Persiapanmu!

Contoh Soal PM UTBK 2023 – Topik #1 untuk soal no 1 sampai 4!

Dalam suatu kelas terdapat 12 murid laki-laki dan 16 murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah 80. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kedapa 4 murid dengan nilai masing-masing 52, 56, 62, dan 66 untuk melakukan remidial. Diketahui bahwa nilai rata-rata peserta naik 7 poin.

Soal 1

Jika sebelum remidial, rata-rata nilai ulangan murid laki-laki di kelas tersebut adalah 78, rata-rata nilai ulangan murid perempuan adalah ….
(A) 80,5
(B) 81
(C) 81,5
(D) 82
(E) 82,5

Pembahasan:
Rata-rata sama dengan jumlah semua nilai dibagi banyak data. Untuk rata-rata gabungan dua data kelompok menggunakan rumus n₁ · x̅₁ + n₂ · x̅₂ = (n₁ + n₂) · x̅.

Dari soal diketahui:

• Rata-rata nilai ulangan Matematika di kelas: x̅ = 80
• Rata-rata nilai ulangan murid laki-laki sebelum remidial: x̅_L = 78
• Banyak murid laki-laki: n_L = 12
• Banyak murid perempuan: n_P = 16

Tanya:
Rata-rata nilai ulangan perempuan sebelum remidial: x̅_P?

Menghitung x̅_P:

x̅_L · x̅₁ + n_P · x̅_P = (n₁ + n₂) · x

12 × 78 + 16 × x̅_P = (12 + 16) × 80

936 + 16x̅_P = 2.240

16x̅_P = 2.240 – 936 = 1.304

Jadi, rata-rata nilai ulangan murid perempuan adalah 81,5 (C).

Soal 2

Diberikan pernyataan berikut.

1) Rata-rata nilai kelas tanpa memperhitungkan keempat murid yang mengikuti remidial adalah 83,5

2) Sebelum remidial, rata-rata nilai ulangan murid yang mengikuti remidial adalah 60

3) Setelah remidial, rata-rata nilai ulangan seluruh murid menjadi 81

4) Jangkauan data nilai murid yang mengikuti remidial adalah 15

Pernyataan di atas yang benar adalah ….
(A) 1), 2), dan 3)
(B) 1) dan 3)
(C) 2) dan 4)
(D) 4)
(E) 1), 2), 3), dan 4)

Pembahasan:

Pernyataan (1): Rata-rata nilai kelas tanpa memperhitungkan keempat murid yang mengikuti remidial adalah 83,5

Diketahui:

• Jumlah siswa: n = 12 + 16 = 28
• Rata-rata kelas = 80
• Jumlah nilai 4 murid yang mengikuti remidial = 52 + 56 + 62 + 66 = 236
• Banyak siswa yang tidak mengikuti remidial = 28 – 4 = 24

Misalkan: x̅_NR = rata-rata 24 siswa yang tidak mengikuti remidial

Maka,

24 × x̅_NR + 236 = 28×80

24x̅_NR + 236 = 2.240

Kesimpulan: Pernyataan (1) BENAR

Pernyataan (2): Sebelum remidial, rata-rata nilai ulangan murid yang mengikuti remidial adalah 60

Rata-rata 4 siswa yang remidial:

Kesimpulan: Pernyataan (2) SALAH

Pernyataan (3): Setelah remidial, rata-rata nilai ulangan seluruh murid menjadi 81

Jumlah siswa: n = 28
Rata-rata kelas: x̅ = 80

Diketahui nilai rata-rata setiap peserta yang remidial naik naik 7 poin. Misal rata-rata siswa setelah remidial = x̅_A, sehingga:

Kesimpulan: Pernyataan (3) BENAR

Pernyataan (4): Jangkauan data nilai murid yang mengikuti remidial adalah 15

Jangkauan tidak bisa dihitung karena data nilai hasil remidial tidak diketahui pasti. Sehingga tidak dapat dipastikan bahwa nilai jangkauan sama dengan 15.

Kesimpulan: Pernyataan (4) tidak diketahui kebenarannya

Jadi, pernyataan yang benar dari empat pernyataan yang diberikan adalah pernyataan 1 dan 3 (B)

Soal 3

Akan dipilih pengurus inti kelas yang terdiri dari 5 murid. Berilah tanda pada kolom yang sesuai.

Pernyataan	Benar	Salah
Banyaknya cara memilih sehingga semua pengurus inti merupakan murid perempuan adalah 4.368
Banyaknya cara memiliki sehingga semua pengurus inti merupakan murid laki-laki adalah 495
Banyaknya cara memiliki sehingga terdapat 2 murid laki-laki sebagai pengurus inti adalah 36.960

Pembahasan: 
Banyak cara memilih banyak m murid perempuan dan n murid laki-laki sebagai pengurus inti dihitung dengan rumus kombinasi.

Banyak cara memilih 5 dari 16 murid perempuan:

Banyak cara memilih 5 dari 12 murid laki-laki

Banyak cara memilih 2 murid laki-laki dan 3 murid perempuan:

= 6 · 11 · 8 · 5 · 14 = 36.960

Jadi, jawabannya adalah Benar ‒ Salah ‒ Benar

Soal 4

Akan dipilih pengurus inti kelas yang terdiri dari 5 murid. Peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti adalah ….

Pembahasan:
Dari soal diketahui,
*Banyak murid laki-laki: n_L = 12
*Banyak murid perempuan: n_P = 16

Kejadian yang dicari adalah pengurus inti dengan satu atau dua murid laki-laki. Sehingga ada dua kemungkinan. Yaitu pengurus inti terdiri dari 1 laki-laki dan 4 perempuan atau 2 laki-laki dan 3 perempuan.

Banyak cara memiliki 1 murid laki-laki dan 4 perempuan:

= 12·4·5·7·13 = 21.840

Banyak cara memilih 2 murid laki-laki dan 3 perempuan:

= 6·11·8·5·14 = 36.960

Sehingga banyak cara memilih satu atau dua murid laki-laki sebagai pengurus inti = 21.840 + 36.960 = 58.800.

Banyak cara memilih 5 pengurus inti:

= 7·27·26·5·4 = 98.280

Besar peluang kejadian:

Contoh Soal PM UTBK 2023 – Topik #2

Kambing ditempatkan dalam kandang pada suatu halaman penuh rumput. Kandang berbentuk persegi panjang ABCD dengan panjang AB = 12 meter dan lebar AD = 9 meter. Kambing ditambatkan pada dinding AB dengan tali yang panjangnya t meter. Pangkal tali ditambatkan pada dinding AB di titik P berjarak x meter dari titik sudut A.

Soal 5

Jika diketahui bahwa 0 < t < 6 meter, daerah merumput kambing akan maksimal jika ….
(A) ^t/₂ ≤ x ≤ 6 + ^t/₂
(B) 6 ‒ t ≤ x ≤ 12 ‒ t 
(C) ^t/₂ ≤ x ≤ 6 + t 
(D) t ≤ x ≤ 6 + t
(E) t ≤ x ≤ 12 ‒ t

Pembahasan: 
Daerah meremput akan maksimal berupa wilayah setengah lingkaran. Titik P terletak pada garis AB dengan panjang AB = 12 m.

Misalkan letak titik P dari titik A (atau titik B) = x m. Maka minimum jarak titik P ke titik A adalah panjang tali kambing, yaitu t m. Dan maksimum jarak titik P ke titik A adalah 12 – t m. Dengan begitu daerah merupmputnya dapat berupa area setengah lingkaran.

Maka letak titik P seharusnya berada di antara t dan 12 – t. Jadi, daerah merumput kambing akan maksimal jika t ≤ x ≤ 12 ‒ t (E).

Soal 6

Misalkan AP = x = 3 meter dan panjang tali untuk kambing pertama adalah t meter, t ≤ 9. Kambing kedua ditempatkan dalam kandang diikat dengan tali yang ditambatkan ke titik Q di dinding BC. Peternak kambing perlu meyakinkan bahwa kedua kambing tidak bertemu dan berebut rumput.

Jika BQ = 6 meter, panjang tali untuk kambing kedua tidak boleh lebih dari … meter.
(A) √72 ‒ t
(B) √117 ‒ t
(C) √131 ‒ t
(D) √145 ‒ t
(E) √180 ‒ t

Pembahasan:
Titik P berada pada sisi AB = 12 meter dan titik Q berada di sisi BC = 9 meter. Jarak titik P ke titik Q adalah dapat dihitung dengan rumus Pythagoras seperti perhitungan berikut.

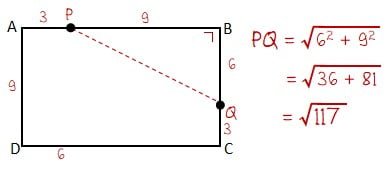
Jumlah panjang kedua tali tidak boleh melebih PQ = √117 m. Jadi panjang tali kambing kedua tidak boleh lebih dari √117 ‒ t meter (B).

Soal 7

Misalkan tali kambing pertama ditambatkan di titik A dan tali kambing kedua di titik C. Panjang tali kambing pertama adalah t meter, dengan 6 ≤ t ≤ 9. Jika panjang tali kambing kedua adalah maksimal sehingga kedua kambing tidak bertemu, jumlah luas daerah merumput kedua kambing akan mencapai nilai maksimum untuk t = ….
(A) 6
(B) 7
(C) 7,5
(D) 8,5
(E) 9

Pembahasan:
Jarak titik A ke titik C sama dengan panjang diagonal ABCD yaitu AC = √(12² + 9²) = √225 = 15 meter. Kedua kambing tidak boleh bertemu. Untuk panjang tali kambing pertama = t, panjang tali kambing kedua harus kurang dari 15 ‒ t meter.

Daerah merumput kedua kambing maksimal berupa seperempat lingkaran. Panjang tali kambing pertama adalah t, maka panjang tali kambing kedua adalah 15 ‒ 7.

Jumlah daerah merumput kambing sama dengan jumlah luas seperempat lingkaran dengan jari-jari t m dan 15 – t m.

Sehingga,